Publications
Papers
-
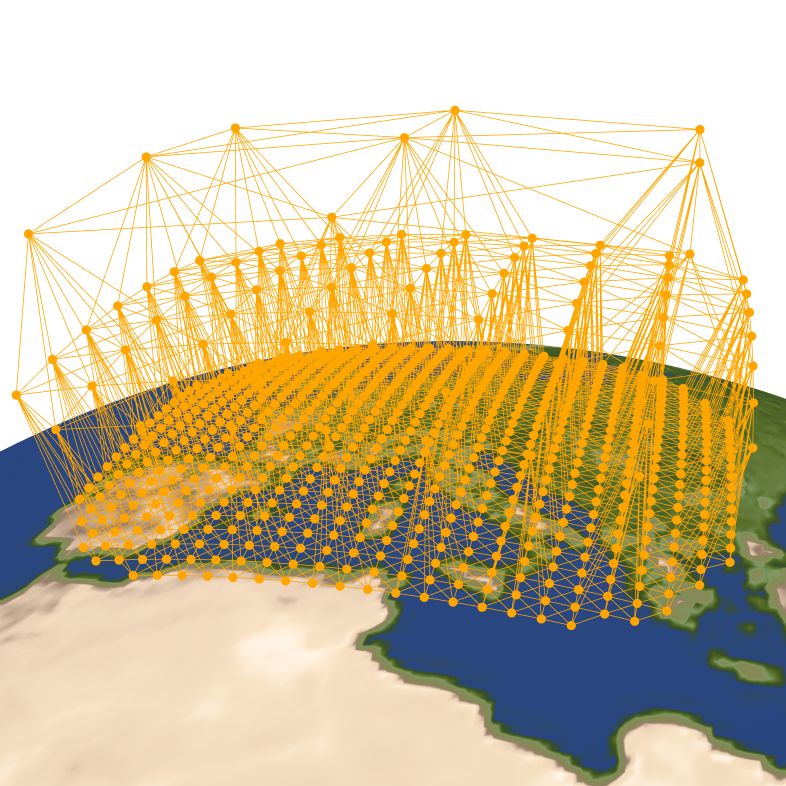 Building Machine Learning Limited Area Models: Kilometer-Scale Weather Forecasting in Realistic SettingsSimon Adamov*, Joel Oskarsson*, Leif Denby, Tomas Landelius, Kasper Hintz, Simon Christiansen, Irene Schicker, Carlos Osuna, Fredrik Lindsten, Oliver Fuhrer, and Sebastian SchemmarXiv preprint, 2025
Building Machine Learning Limited Area Models: Kilometer-Scale Weather Forecasting in Realistic SettingsSimon Adamov*, Joel Oskarsson*, Leif Denby, Tomas Landelius, Kasper Hintz, Simon Christiansen, Irene Schicker, Carlos Osuna, Fredrik Lindsten, Oliver Fuhrer, and Sebastian SchemmarXiv preprint, 2025Machine learning is revolutionizing global weather forecasting, with models that efficiently produce highly accurate forecasts. Apart from global forecasting there is also a large value in high-resolution regional weather forecasts, focusing on accurate simulations of the atmosphere for a limited area. Initial attempts have been made to use machine learning for such limited area scenarios, but these experiments do not consider realistic forecasting settings and do not investigate the many design choices involved. We present a framework for building kilometer-scale machine learning limited area models with boundary conditions imposed through a flexible boundary forcing method. This enables boundary conditions defined either from reanalysis or operational forecast data. Our approach employs specialized graph constructions with rectangular and triangular meshes, along with multi-step rollout training strategies to improve temporal consistency. We perform systematic evaluation of different design choices, including the boundary width, graph construction and boundary forcing integration. Models are evaluated across both a Danish and a Swiss domain, two regions that exhibit different orographical characteristics. Verification is performed against both gridded analysis data and in-situ observations, including a case study for the storm Ciara in February 2020. Both models achieve skillful predictions across a wide range of variables, with our Swiss model outperforming the numerical weather prediction baseline for key surface variables. With their substantially lower computational cost, our findings demonstrate great potential for machine learning limited area models in the future of regional weather forecasting.
@article{adamov2025building, title = {Building Machine Learning Limited Area Models: Kilometer-Scale Weather Forecasting in Realistic Settings}, author = {Adamov, Simon and Oskarsson, Joel and Denby, Leif and Landelius, Tomas and Hintz, Kasper and Christiansen, Simon and Schicker, Irene and Osuna, Carlos and Lindsten, Fredrik and Fuhrer, Oliver and Schemm, Sebastian}, journal = {arXiv preprint}, year = {2025}, } -
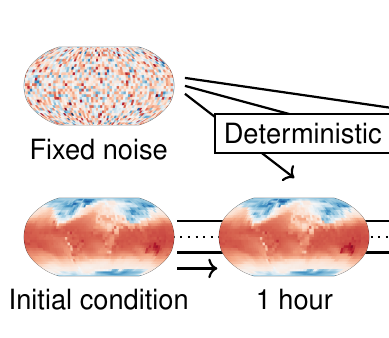 Continuous Ensemble Weather Forecasting with Diffusion modelsIn International Conference on Learning Representations, 2025
Continuous Ensemble Weather Forecasting with Diffusion modelsIn International Conference on Learning Representations, 2025Weather forecasting has seen a shift in methods from numerical simulations to data-driven systems. While initial research in the area focused on deterministic forecasting, recent works have used diffusion models to produce skillful ensemble forecasts. These models are trained on a single forecasting step and rolled out autoregressively. However, they are computationally expensive and accumulate errors for high temporal resolution due to the many rollout steps. We address these limitations with Continuous Ensemble Forecasting, a novel and flexible method for sampling ensemble forecasts in diffusion models. The method can generate temporally consistent ensemble trajectories completely in parallel, with no autoregressive steps. Continuous Ensemble Forecasting can also be combined with autoregressive rollouts to yield forecasts at an arbitrary fine temporal resolution without sacrificing accuracy. We demonstrate that the method achieves competitive results for global weather forecasting with good probabilistic properties.
@inproceedings{andrae2024continuousensembleweatherforecasting, title = {Continuous Ensemble Weather Forecasting with Diffusion models}, author = {Andrae, Martin and Landelius, Tomas and Oskarsson, Joel and Lindsten, Fredrik}, booktitle = {International Conference on Learning Representations}, year = {2025}, } -
 Probabilistic Weather Forecasting with Hierarchical Graph Neural NetworksIn Advances in Neural Information Processing Systems, 2024Spotlight
Probabilistic Weather Forecasting with Hierarchical Graph Neural NetworksIn Advances in Neural Information Processing Systems, 2024SpotlightIn recent years, machine learning has established itself as a powerful tool for high-resolution weather forecasting. While most current machine learning models focus on deterministic forecasts, accurately capturing the uncertainty in the chaotic weather system calls for probabilistic modeling. We propose a probabilistic weather forecasting model called Graph-EFM, combining a flexible latent-variable formulation with the successful graph-based forecasting framework. The use of a hierarchical graph construction allows for efficient sampling of spatially coherent forecasts. Requiring only a single forward pass per time step, Graph-EFM allows for fast generation of arbitrarily large ensembles. We experiment with the model on both global and limited area forecasting. Ensemble forecasts from Graph-EFM achieve equivalent or lower errors than comparable deterministic models, with the added benefit of accurately capturing forecast uncertainty.
@inproceedings{oskarsson2024probabilistic, title = {Probabilistic Weather Forecasting with Hierarchical Graph Neural Networks}, author = {Oskarsson, Joel and Landelius, Tomas and Deisenroth, Marc Peter and Lindsten, Fredrik}, year = {2024}, booktitle = {Advances in Neural Information Processing Systems}, volume = {37}, } -
 Uncertainty Quantification of Pre-Trained and Fine-Tuned Surrogate Models using Conformal PredictionVignesh Gopakumar, Ander Gray, Joel Oskarsson, Lorenzo Zanisi, Stanislas Pamela, Daniel Giles, Matt Kusner, and Marc Peter DeisenrotharXiv preprint, 2024
Uncertainty Quantification of Pre-Trained and Fine-Tuned Surrogate Models using Conformal PredictionVignesh Gopakumar, Ander Gray, Joel Oskarsson, Lorenzo Zanisi, Stanislas Pamela, Daniel Giles, Matt Kusner, and Marc Peter DeisenrotharXiv preprint, 2024Data-driven surrogate models have shown immense potential as quick, inexpensive approximations to complex numerical and experimental modelling tasks. However, most surrogate models characterising physical systems do not quantify their uncertainty, rendering their predictions unreliable, and needing further validation. Though Bayesian approximations offer some solace in estimating the error associated with these models, they cannot provide they cannot provide guarantees, and the quality of their inferences depends on the availability of prior information and good approximations to posteriors for complex problems. This is particularly pertinent to multi-variable or spatio-temporal problems. Our work constructs and formalises a conformal prediction framework that satisfies marginal coverage for spatio-temporal predictions in a model-agnostic manner, requiring near-zero computational costs. The paper provides an extensive empirical study of the application of the framework to ascertain valid error bars that provide guaranteed coverage across the surrogate model’s domain of operation. The application scope of our work extends across a large range of spatio-temporal models, ranging from solving partial differential equations to weather forecasting. Through the applications, the paper looks at providing statistically valid error bars for deterministic models, as well as crafting guarantees to the error bars of probabilistic models. The paper concludes with a viable conformal prediction formalisation that provides guaranteed coverage of the surrogate model, regardless of model architecture, and its training regime and is unbothered by the curse of dimensionality.
@article{gopakumar2024uncertainty, title = {Uncertainty Quantification of Pre-Trained and Fine-Tuned Surrogate Models using Conformal Prediction}, author = {Gopakumar, Vignesh and Gray, Ander and Oskarsson, Joel and Zanisi, Lorenzo and Pamela, Stanislas and Giles, Daniel and Kusner, Matt and Deisenroth, Marc Peter}, journal = {arXiv preprint}, year = {2024}, } -
 MTP-GO: Graph-Based Probabilistic Multi-Agent Trajectory Prediction with Neural ODEsTheodor Westny, Joel Oskarsson, Björn Olofsson, and Erik FriskIEEE Transactions on Intelligent Vehicles, 2023
MTP-GO: Graph-Based Probabilistic Multi-Agent Trajectory Prediction with Neural ODEsTheodor Westny, Joel Oskarsson, Björn Olofsson, and Erik FriskIEEE Transactions on Intelligent Vehicles, 2023Enabling resilient autonomous motion planning requires robust predictions of surrounding road users’ future behavior. In response to this need and the associated challenges, we introduce our model, titled MTP-GO. The model encodes the scene using temporal graph neural networks to produce the inputs to an underlying motion model. The motion model is implemented using neural ordinary differential equations where the state-transition functions are learned with the rest of the model. Multi-modal probabilistic predictions are provided by combining the concept of mixture density networks and Kalman filtering. The results illustrate the predictive capabilities of the proposed model across various data sets, outperforming several state-of-the-art methods on a number of metrics.
@article{westny2023graph, journal = {IEEE Transactions on Intelligent Vehicles}, title = {MTP-GO: Graph-Based Probabilistic Multi-Agent Trajectory Prediction with Neural ODEs}, year = {2023}, author = {Westny, Theodor and Oskarsson, Joel and Olofsson, Bj{\"o}rn and Frisk, Erik}, } -
 Evaluation of Differentially Constrained Motion Models for Graph-Based Trajectory PredictionTheodor Westny, Joel Oskarsson, Björn Olofsson, and Erik FriskIn 2023 IEEE Intelligent Vehicles Symposium (IV), 2023
Evaluation of Differentially Constrained Motion Models for Graph-Based Trajectory PredictionTheodor Westny, Joel Oskarsson, Björn Olofsson, and Erik FriskIn 2023 IEEE Intelligent Vehicles Symposium (IV), 2023Given their flexibility and encouraging performance, deep-learning models are becoming standard for motion prediction in autonomous driving. However, with great flexibility comes a lack of interpretability and possible violations of physical constraints. Accompanying these data-driven methods with differentially-constrained motion models to provide physically feasible trajectories is a promising future direction. The foundation for this work is a previously introduced graph-neural-network-based model, MTP-GO. The neural network learns to compute the inputs to an underlying motion model to provide physically feasible trajectories. This research investigates the performance of various motion models in combination with numerical solvers for the prediction task. The study shows that simpler models, such as low-order integrator models, are preferred over more complex, e.g., kinematic models, to achieve accurate predictions. Further, the numerical solver can have a substantial impact on performance, advising against commonly used first-order methods like Euler forward. Instead, a second-order method like Heun’s can greatly improve predictions.
@inproceedings{westny2023evaluation, title = {Evaluation of Differentially Constrained Motion Models for Graph-Based Trajectory Prediction}, author = {Westny, Theodor and Oskarsson, Joel and Olofsson, Bj{\"o}rn and Frisk, Erik}, booktitle = {2023 IEEE Intelligent Vehicles Symposium (IV)}, year = {2023}, } -
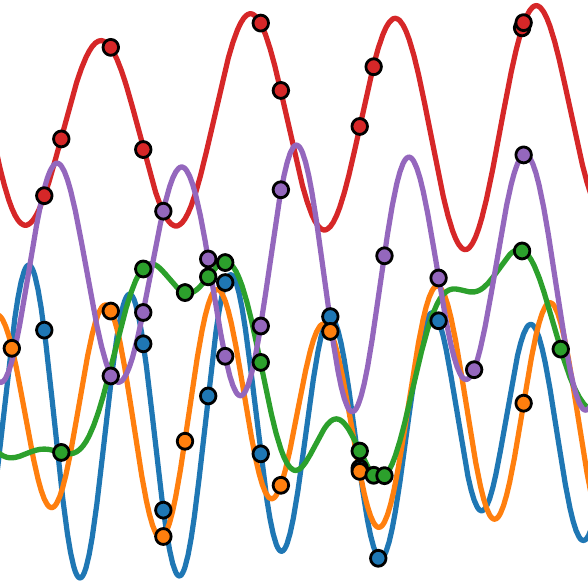 Temporal Graph Neural Networks for Irregular DataJoel Oskarsson, Per Sidén, and Fredrik LindstenIn Proceedings of The 26th International Conference on Artificial Intelligence and Statistics, 2023
Temporal Graph Neural Networks for Irregular DataJoel Oskarsson, Per Sidén, and Fredrik LindstenIn Proceedings of The 26th International Conference on Artificial Intelligence and Statistics, 2023This paper proposes a temporal graph neural network model for forecasting of graph-structured irregularly observed time series. Our TGNN4I model is designed to handle both irregular time steps and partial observations of the graph. This is achieved by introducing a time-continuous latent state in each node, following a linear Ordinary Differential Equation (ODE) defined by the output of a Gated Recurrent Unit (GRU). The ODE has an explicit solution as a combination of exponential decay and periodic dynamics. Observations in the graph neighborhood are taken into account by integrating graph neural network layers in both the GRU state update and predictive model. The time-continuous dynamics additionally enable the model to make predictions at arbitrary time steps. We propose a loss function that leverages this and allows for training the model for forecasting over different time horizons. Experiments on simulated data and real-world data from traffic and climate modeling validate the usefulness of both the graph structure and time-continuous dynamics in settings with irregular observations.
@inproceedings{tgnn4i, title = {Temporal Graph Neural Networks for Irregular Data}, author = {Oskarsson, Joel and Sid\'en, Per and Lindsten, Fredrik}, booktitle = {Proceedings of The 26th International Conference on Artificial Intelligence and Statistics}, pages = {4515--4531}, year = {2023}, editor = {Ruiz, Francisco and Dy, Jennifer and van de Meent, Jan-Willem}, volume = {206}, series = {Proceedings of Machine Learning Research}, publisher = {PMLR}, } -
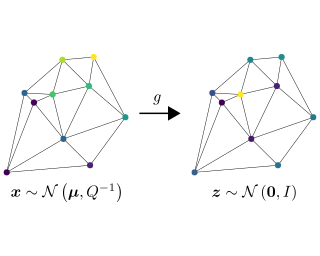 Scalable Deep Gaussian Markov Random Fields for General GraphsJoel Oskarsson, Per Sidén, and Fredrik LindstenIn Proceedings of the 39th International Conference on Machine Learning, 2022
Scalable Deep Gaussian Markov Random Fields for General GraphsJoel Oskarsson, Per Sidén, and Fredrik LindstenIn Proceedings of the 39th International Conference on Machine Learning, 2022Machine learning methods on graphs have proven useful in many applications due to their ability to handle generally structured data. The framework of Gaussian Markov Random Fields (GMRFs) provides a principled way to define Gaussian models on graphs by utilizing their sparsity structure. We propose a flexible GMRF model for general graphs built on the multi-layer structure of Deep GMRFs, originally proposed for lattice graphs only. By designing a new type of layer we enable the model to scale to large graphs. The layer is constructed to allow for efficient training using variational inference and existing software frameworks for Graph Neural Networks. For a Gaussian likelihood, close to exact Bayesian inference is available for the latent field. This allows for making predictions with accompanying uncertainty estimates. The usefulness of the proposed model is verified by experiments on a number of synthetic and real world datasets, where it compares favorably to other both Bayesian and deep learning methods.
@inproceedings{pmlr-v162-oskarsson22a, title = {Scalable Deep {G}aussian {M}arkov Random Fields for General Graphs}, author = {Oskarsson, Joel and Sid{\'e}n, Per and Lindsten, Fredrik}, booktitle = {Proceedings of the 39th International Conference on Machine Learning}, pages = {17117--17137}, year = {2022}, editor = {Chaudhuri, Kamalika and Jegelka, Stefanie and Song, Le and Szepesvari, Csaba and Niu, Gang and Sabato, Sivan}, volume = {162}, series = {Proceedings of Machine Learning Research}, publisher = {PMLR}, url = {https://proceedings.mlr.press/v162/oskarsson22a.html}, }
Workshop papers
-
 CRPS-LAM: Regional ensemble weather forecasting from matching marginalsIn EurIPS 2025 Workshop on AI for Climate and Conservation, 2025
CRPS-LAM: Regional ensemble weather forecasting from matching marginalsIn EurIPS 2025 Workshop on AI for Climate and Conservation, 2025Machine learning for weather prediction increasingly relies on ensemble methods to provide probabilistic forecasts. Diffusion-based models have shown strong performance in Limited-Area Modeling (LAM) but remain computationally expensive at sampling time. Building on the success of global weather forecasting models trained based on Continuous Ranked Probability Score (CRPS), we introduce CRPS-LAM, a probabilistic LAM forecasting model trained with a CRPS-based objective. By sampling and injecting a single latent noise vector into the model, CRPS-LAM generates ensemble members in a single forward pass, achieving sampling speeds up to 39 times faster than a diffusion-based model. We evaluate the model on the MEPS regional dataset, where CRPS-LAM matches the low errors of diffusion models. By retaining also fine-scale forecast details, the method stands out as an effective approach for probabilistic regional weather forecasting
@inproceedings{larsson2025crps, title = {CRPS-LAM: Regional ensemble weather forecasting from matching marginals}, author = {Larsson, Erik and Oskarsson, Joel and Landelius, Tomas and Lindsten, Fredrik}, booktitle = {EurIPS 2025 Workshop on AI for Climate and Conservation}, year = {2025}, } -
 Diffusion-LAM: Probabilistic Limited Area Weather Forecasting with DiffusionIn ICLR 2025 Workshop on Tackling Climate Change with Machine Learning, 2025
Diffusion-LAM: Probabilistic Limited Area Weather Forecasting with DiffusionIn ICLR 2025 Workshop on Tackling Climate Change with Machine Learning, 2025Machine learning methods have been shown to be effective for weather forecasting, based on the speed and accuracy compared to traditional numerical models. While early efforts primarily concentrated on deterministic predictions, the field has increasingly shifted toward probabilistic forecasting to better capture the forecast uncertainty. Most machine learning-based models have been designed for global-scale predictions, with only limited work targeting regional or limited area forecasting, which allows more specialized and flexible modeling for specific locations. This work introduces Diffusion-LAM, a probabilistic limited area weather model leveraging conditional diffusion. By conditioning on boundary data from surrounding regions, our approach generates forecasts within a defined area. Experimental results on the MEPS limited area dataset demonstrate the potential of Diffusion-LAM to deliver accurate probabilistic forecasts, highlighting its promise for limited-area weather prediction.
@inproceedings{larsson2025diffusion, title = {Diffusion-LAM: Probabilistic Limited Area Weather Forecasting with Diffusion}, author = {Larsson, Erik and Oskarsson, Joel and Landelius, Tomas and Lindsten, Fredrik}, booktitle = {ICLR 2025 Workshop on Tackling Climate Change with Machine Learning}, year = {2025}, } -
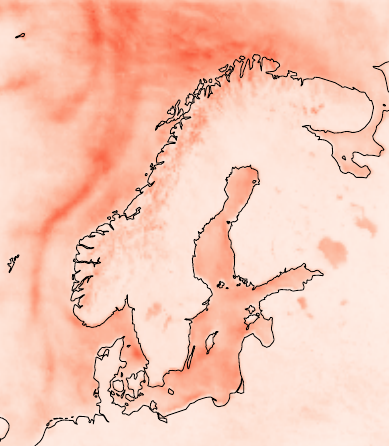 Valid Error Bars for Neural Weather Models using Conformal PredictionVignesh Gopakumar, Joel Oskarsson, Ander Gray, Lorenzo Zanisi, Stanislas Pamela, Daniel Giles, Matt Kusner, and Marc DeisenrothIn ICML Workshop on Machine Learning for Earth System Modeling, 2024Note: A substantial extension of this research is presented in our paper "Uncertainty Quantification of Pre-Trained and Fine-Tuned Surrogate Models using Conformal Prediction"
Valid Error Bars for Neural Weather Models using Conformal PredictionVignesh Gopakumar, Joel Oskarsson, Ander Gray, Lorenzo Zanisi, Stanislas Pamela, Daniel Giles, Matt Kusner, and Marc DeisenrothIn ICML Workshop on Machine Learning for Earth System Modeling, 2024Note: A substantial extension of this research is presented in our paper "Uncertainty Quantification of Pre-Trained and Fine-Tuned Surrogate Models using Conformal Prediction"Neural weather models have shown immense potential as inexpensive and accurate alternatives to physics-based models. However, most models trained to perform weather forecasting do not quantify the uncertainty associated with their forecasts. This limits the trust in the model and the usefulness of the forecasts. In this work we construct and formalise a conformal prediction framework as a post-processing method for estimating this uncertainty. The method is model-agnostic and gives calibrated error bounds for all variables, lead times and spatial locations. No modifications are required to the model and the computational cost is negligible compared to model training. We demonstrate the usefulness of the conformal prediction framework on a limited area neural weather model for the Nordic region. We further explore the advantages of the framework for deterministic and probabilistic models.
@inproceedings{gopakumar2024valid, title = {Valid Error Bars for Neural Weather Models using Conformal Prediction}, booktitle = {ICML Workshop on Machine Learning for Earth System Modeling}, author = {Gopakumar, Vignesh and Oskarsson, Joel and Gray, Ander and Zanisi, Lorenzo and Pamela, Stanislas and Giles, Daniel and Kusner, Matt and Deisenroth, Marc}, year = {2024}, } -
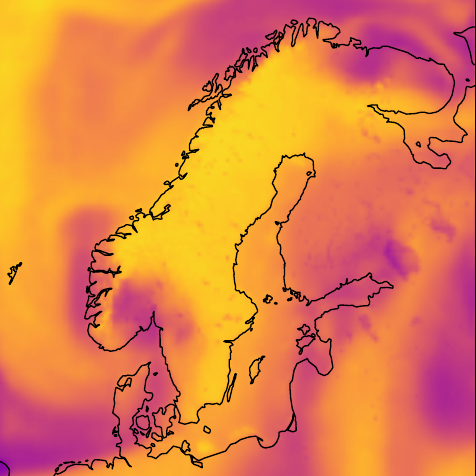 Graph-based Neural Weather Prediction for Limited Area ModelingJoel Oskarsson, Tomas Landelius, and Fredrik LindstenIn NeurIPS 2023 Workshop on Tackling Climate Change with Machine Learning, 2023
Graph-based Neural Weather Prediction for Limited Area ModelingJoel Oskarsson, Tomas Landelius, and Fredrik LindstenIn NeurIPS 2023 Workshop on Tackling Climate Change with Machine Learning, 2023The rise of accurate machine learning methods for weather forecasting is creating radical new possibilities for modeling the atmosphere. In the time of climate change, having access to high-resolution forecasts from models like these is also becoming increasingly vital. While most existing Neural Weather Prediction (NeurWP) methods focus on global forecasting, an important question is how these techniques can be applied to limited area modeling. In this work we adapt the graph-based NeurWP approach to the limited area setting and propose a multi-scale hierarchical model extension. Our approach is validated by experiments with a local model for the Nordic region.
@inproceedings{oskarsson2023graphbased, title = {Graph-based Neural Weather Prediction for Limited Area Modeling}, author = {Oskarsson, Joel and Landelius, Tomas and Lindsten, Fredrik}, booktitle = {NeurIPS 2023 Workshop on Tackling Climate Change with Machine Learning}, year = {2023}, } -
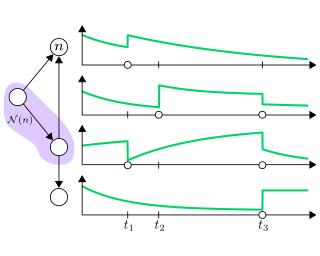 Temporal Graph Neural Networks with Time-Continuous Latent StatesJoel Oskarsson, Per Sidén, and Fredrik LindstenIn ICML Workshop on Continuous Time Methods for Machine Learning, 2022Note: A substantial extension of this research is presented in our paper "Temporal Graph Neural Networks for Irregular Data"
Temporal Graph Neural Networks with Time-Continuous Latent StatesJoel Oskarsson, Per Sidén, and Fredrik LindstenIn ICML Workshop on Continuous Time Methods for Machine Learning, 2022Note: A substantial extension of this research is presented in our paper "Temporal Graph Neural Networks for Irregular Data"We propose a temporal graph neural network model for graph-structured irregular time series. The model is designed to handle both irregular time steps and partial graph observations. This is achieved by introducing a time-continuous latent state in each node of the graph. The latent dynamics are defined using a state-dependent decay-mechanism. Observations in the graph neighborhood are taken into account by integrating graph neural network layers in both the state update and predictive model. Experiments on a traffic forecasting task validate the usefulness of both the graph structure and time-continuous dynamics in this setting.
@inproceedings{temporal_continuous_gnns, author = {Oskarsson, Joel and Sid{\'e}n, Per and Lindsten, Fredrik}, title = {Temporal Graph Neural Networks with Time-Continuous Latent States}, booktitle = {ICML Workshop on Continuous Time Methods for Machine Learning}, year = {2022}, }
Theses
-
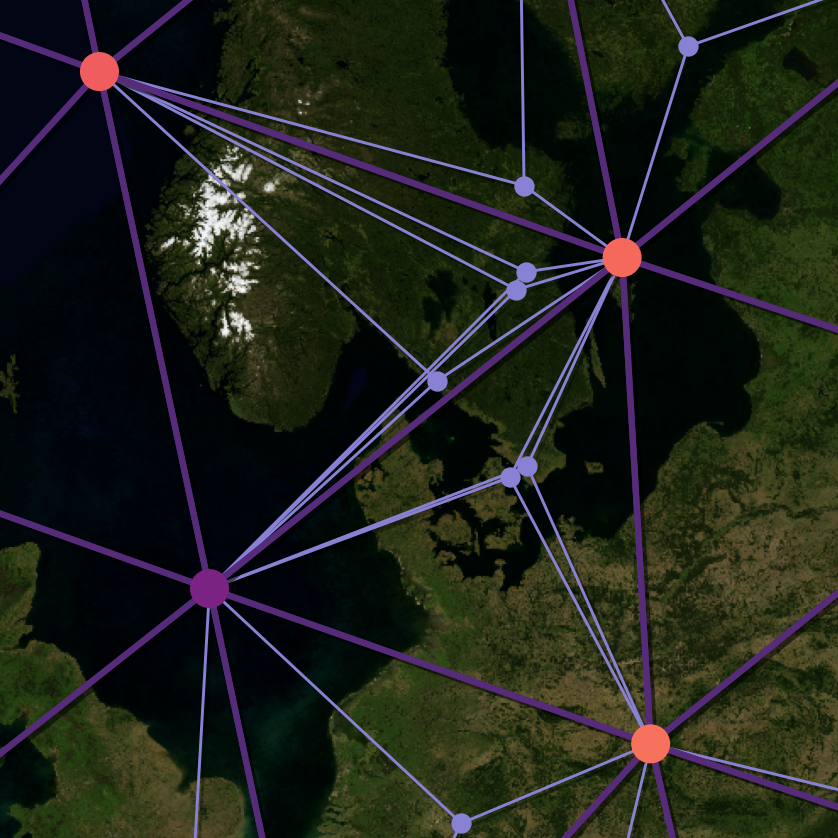 Modeling Spatio-Temporal Systems with Graph-based Machine LearningJoel OskarssonLinköping University, Department of Computer and Information Science, Division of Statistics and Machine Learning, 2025PhD Thesis
Modeling Spatio-Temporal Systems with Graph-based Machine LearningJoel OskarssonLinköping University, Department of Computer and Information Science, Division of Statistics and Machine Learning, 2025PhD ThesisMost systems in the physical world are spatio-temporal in nature. The clouds move over our heads, vehicles travel on the roads and electricity is transmitted through vast spatial networks. Machine learning offers many opportunities to understand and forecast the evolution of these systems by making use of large amounts of collected data. However, building useful models of such systems requires taking both spatial and temporal correlations into account. We can not accurately forecast the weather in Linköping without knowing if there is hot air blowing in from the south. Similarly, we can not predict if a vehicle is about to make a left turn without knowing its position and velocity relative to other vehicles on the road. This thesis proposes a set of methods for accurately capturing such spatio-temporal dependencies in machine learning models.
At the core of the thesis is the idea of using graphs as a way to represent the spatial relationships in spatio-temporal systems. Graphs offer a highly flexible framework for this purpose, in particular for situations where observation locations do not lie on a regular spatial grid. Throughout the thesis, spatial graphs are constructed by letting nodes correspond to spatial locations and edges the relationships between them. These graphs are then used to construct different machine learning models, including graph neural networks and probabilistic graphical models. Combining such graph-based components with machine learning methods for time series modeling then allows for capturing the full spatio-temporal structure of the data.
The main contribution of the thesis lies in exploring a number of methods using graph-based modeling for spatio-temporal data. This includes extending temporal graph neural networks to handle data observed irregularly over time. Temporal graph neural networks are also used to develop a model for vehicle trajectory forecasting, where the edges of the graph correspond to interactions between traffic agents. The thesis additionally includes work on Bayesian modeling, where a connection between Gaussian Markov random fields and graph neural networks allows for building scalable probabilistic models for data defined using graphs.
A motivation for the methods developed in this thesis is the increasing use of machine learning in earth science. Capturing relevant spatio-temporal relationships is central for building useful models of the earth system. The thesis includes numerous experiments making use of weather and climate data, as well as application-driven work specifically targeting weather forecasting. Recent years have seen rapid progress in using machine learning models for weather forecasting, and the thesis makes multiple contributions in this direction. A probabilistic weather forecasting model is developed by combining graph-based methods with a latent variable formulation. Lastly, machine learning limited area models are also explored, where graph neural networks are used for regional weather forecasting.@phdthesis{oskarsson2025modeling, title = {Modeling Spatio-Temporal Systems with Graph-based Machine Learning}, school = {Linköping University, Department of Computer and Information Science, Division of Statistics and Machine Learning}, author = {Oskarsson, Joel}, year = {2025}, } -
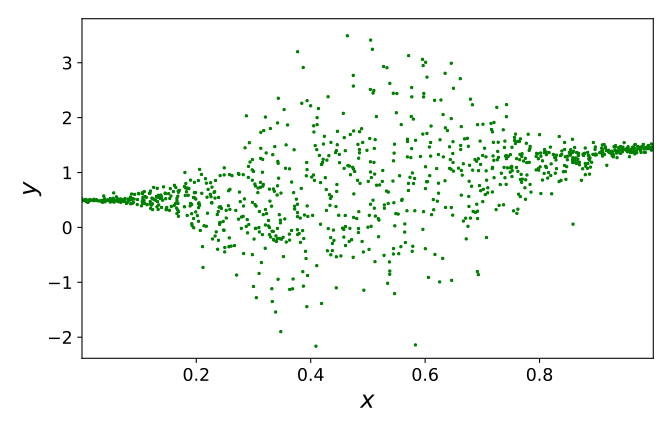 Probabilistic Regression using Conditional Generative Adversarial NetworksJoel OskarssonLinköping University, Department of Computer and Information Science, Division of Statistics and Machine Learning, 2020MSc Thesis
Probabilistic Regression using Conditional Generative Adversarial NetworksJoel OskarssonLinköping University, Department of Computer and Information Science, Division of Statistics and Machine Learning, 2020MSc ThesisRegression is a central problem in statistics and machine learning with applications everywhere in science and technology. In probabilistic regression the relationship between a set of features and a real-valued target variable is modelled as a conditional probability distribution. There are cases where this distribution is very complex and not properly captured by simple approximations, such as assuming a normal distribution. This thesis investigates how conditional Generative Adversarial Networks (GANs) can be used to properly capture more complex conditional distributions. GANs have seen great success in generating complex high-dimensional data, but less work has been done on their use for regression problems. This thesis presents experiments to better understand how conditional GANs can be used in probabilistic regression. Different versions of GANs are extended to the conditional case and evaluated on synthetic and real datasets. It is shown that conditional GANs can learn to estimate a wide range of different distributions and be competitive with existing probabilistic regression models.
@mastersthesis{Oskarsson1442847, author = {Oskarsson, Joel}, pages = {111}, school = {Linköping University, Department of Computer and Information Science, Division of Statistics and Machine Learning}, title = {Probabilistic Regression using Conditional Generative Adversarial Networks}, keywords = {machine learning, ml, regression, probabilistic, distribution, cgan, gan, conditional gan, adversarial networks, neural network, deep learning, f-gan, f-cgan, f-divergence, adversarial training, bimodal, heteroskedastic, mmd, maximum mean discrepancy, gmmn, generative moment matching network, conditional gmmn, ipm, kde, cgan evaluation, cgan regression, gan regression, cgan-regression, regression using gan, deep, nn, implicit, generative, conditional, model, complex noise, aleatoric, uncertainty, dctd, mdn, heteroskedastic regression, gp}, year = {2020}, }