ICML Paper "Scalable Deep Gaussian Markov Random Fields for General Graphs" + Workshop Paper on Temporal GNNs
At ICML this summer I am excited to be presenting one paper at the main conference and one workshop paper. Both works are together with my supervisors Per Sidén and Fredrik Lindsten.
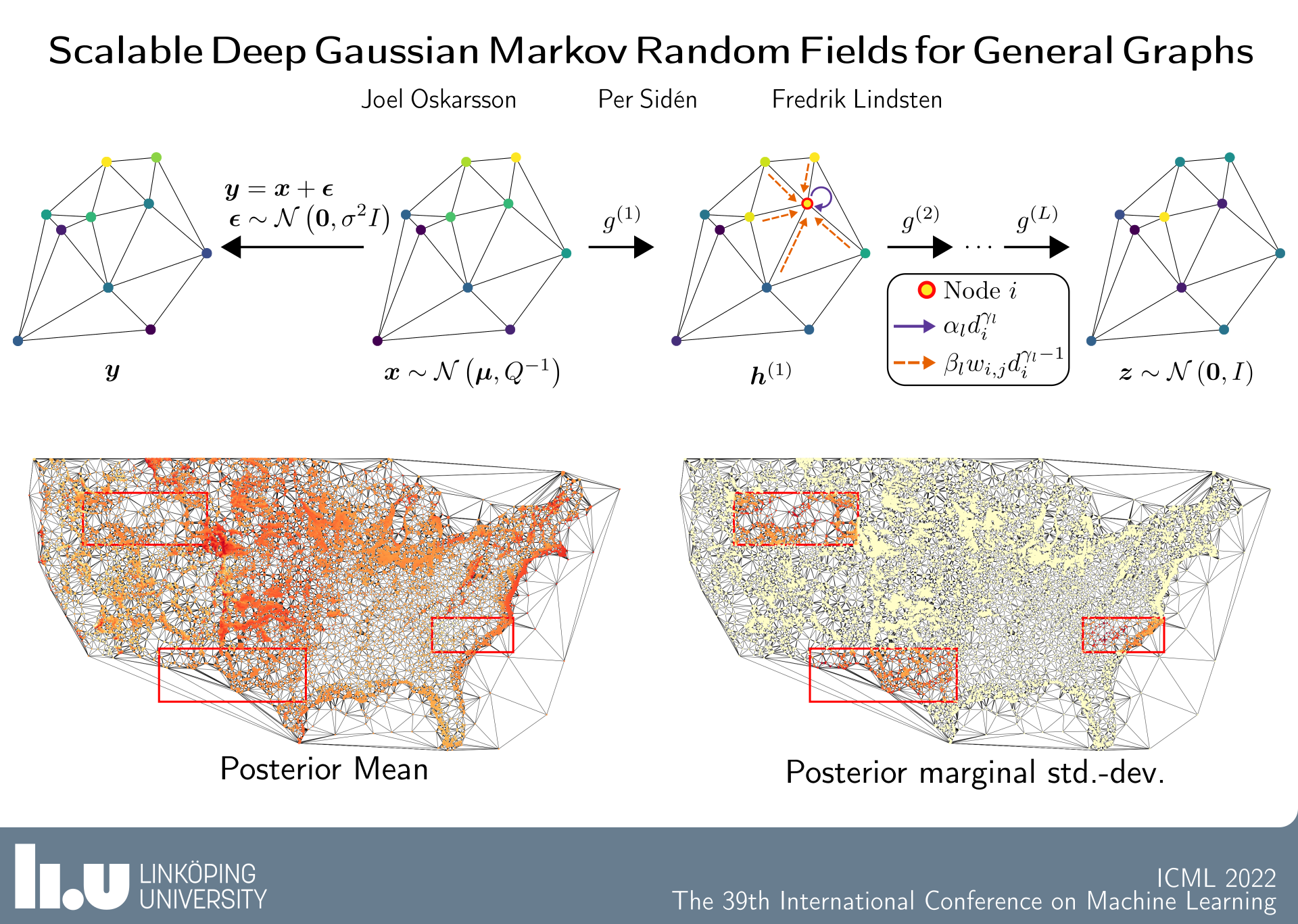
Our paper Scalable Deep Gaussian Markov tandom Fields for General Graphs proposes a scalable Bayesian model for graph-structured data. We build on the Deep GMRF framework and extend this to a general graph setting.
Abstract
Machine learning methods on graphs have proven useful in many applications due to their ability to handle generally structured data. The framework of Gaussian Markov Random Fields (GMRFs) provides a principled way to define Gaussian models on graphs by utilizing their sparsity structure. We propose a flexible GMRF model for general graphs built on the multi-layer structure of Deep GMRFs, originally proposed for lattice graphs only. By designing a new type of layer we enable the model to scale to large graphs. The layer is constructed to allow for efficient training using variational inference and existing software frameworks for Graph Neural Networks. For a Gaussian likelihood, close to exact Bayesian inference is available for the latent field. This allows for making predictions with accompanying uncertainty estimates. The usefulness of the proposed model is verified by experiments on a number of synthetic and real world datasets, where it compares favorably to other both Bayesian and deep learning methods.
Temporal Graph Neural Networks with Time-Continuous Latent States
Additionally, our paper Temporal Graph Neural Networks with Time-Continuous Latent States has been accepted to the ICML Workshop on Continuous Time Methods for Machine Learning. In this work we tackle the problem of irregular observations in temporal graph data. The proposed solution is a temporal GNN model with latent states defined over continuous time.
Abstract
We propose a temporal graph neural network model for graph-structured irregular time series. The model is designed to handle both irregular time steps and partial graph observations. This is achieved by introducing a time-continuous latent state in each node of the graph. The latent dynamics are defined using a state-dependent decay-mechanism. Observations in the graph neighborhood are taken into account by integrating graph neural network layers in both the state update and predictive model. Experiments on a traffic forecasting task validate the usefulness of both the graph structure and time-continuous dynamics in this setting.